苍天远比海更远

四人追逐问题 - Python

四人追逐问题是数学建模比赛中一个经典的问题，通常涉及四个对象在一个平面内互相追逐，形成一种动态的追逐路径。
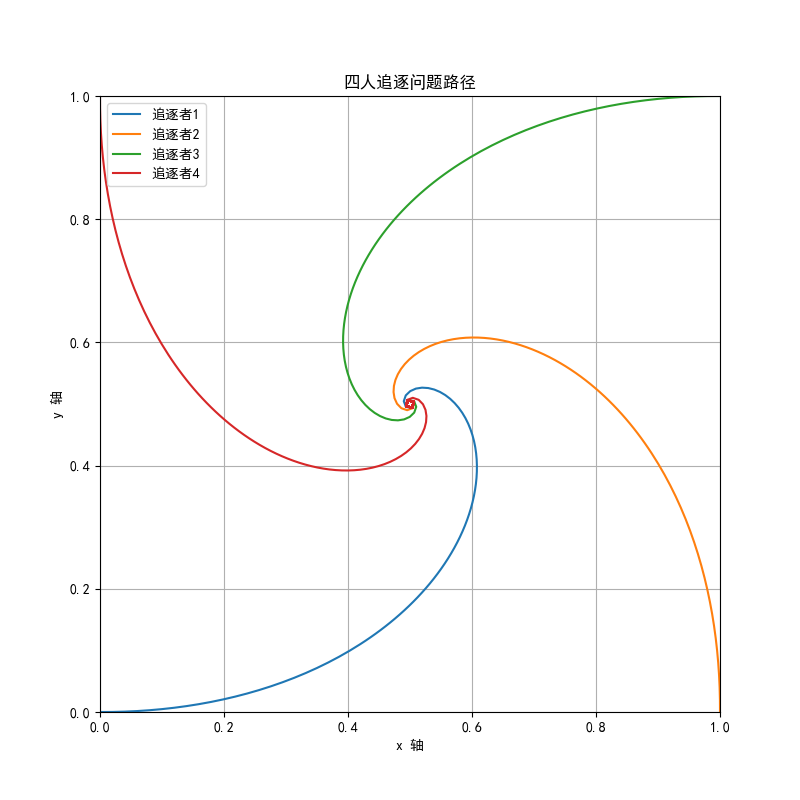
通常的设定是四个追逐者分别位于正方形的四个顶点，每个人以相同的速度一直朝着邻近的那个追逐者前进。
这个问题的数学描述涉及微分方程和几何学，研究这些对象的路径形状、相遇时间，以及相遇地点等。随着时间的推移，追逐者的路径会逐渐变为一个螺旋状，最终四个对象会在正方形的中心相遇。

参考

https://math.nuist.edu.cn/mathlab/3669/list.psp
（南京信息工程大学数学与统计学院数学教育实验中心）

模拟程序

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation, PillowWriter

# 设置字体为 SimHei (黑体)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 初始化四个追逐者的初始位置
positions = np.array([[0, 0], [1, 0], [1, 1], [0, 1]], dtype=float)

# 设定步长和总步数
dt = 0.01
steps = 1000

# 用于保存追逐者路径的数组
trajectories = [positions.copy()]

for _ in range(steps):
    directions = np.zeros_like(positions)
    for i in range(4):
        next_pos = positions[(i + 1) % 4]
        direction = next_pos - positions[i]
        directions[i] = direction / np.linalg.norm(direction)
    positions += dt * directions
    trajectories.append(positions.copy())

# 将路径转换为numpy数组以便于绘制
trajectories = np.array(trajectories)

# 创建图形对象
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
lines = [ax.plot([], [], label=f'追逐者{i + 1}')[0] for i in range(4)]

# 更新函数，用于动画
def update(frame):
    for i, line in enumerate(lines):
        line.set_data(trajectories[:frame, i, 0], trajectories[:frame, i, 1])
    return lines

# 创建动画
ani = FuncAnimation(fig, update, frames=range(1, steps), blit=True, interval=20)

# 设置图形标题和标签
ax.set_title('四人追逐问题路径')
ax.set_xlabel('x 轴')
ax.set_ylabel('y 轴')
ax.legend()
ax.grid(True)

# 保存动画为GIF
gif_writer = PillowWriter(fps=30)
ani.save("four_chase.gif", writer=gif_writer)

# 保存最后一帧为PNG
update(steps - 1)  # 更新到最后一帧
plt.savefig("four_chase.png")

# 显示动画
plt.show()